这是 DeepMind Scaling Book 系列的第 4 部分。

那些你需要知道的 Transformer 数学 (All the Transformer Math You Need to Know)

How To Scale Your Model Part 4 (Part 3: Sharding | Part 5: Training)

在这里，我们将快速回顾 Transformer 架构，特别是如何计算 FLOPs、字节数和其他感兴趣的量。

数点数 (Counting Dots)

让我们从向量 $x, y$ 和矩阵 $A, B$ 开始，形状如下：

\[\def \red#1{\textcolor{red}{#1}} \def \green#1{\textcolor{green}{#1}} \def \blue#1{\textcolor{blue}{#1}} \def \purple#1{\textcolor{purple}{#1}} \def \orange#1{\textcolor{orange}{#1}} \def \gray#1{\textcolor{gray}{#1}} \begin{array}{cc} \textrm{array} & \textrm{shape} \\ \hline x & \textrm{[P]} \\ y & \textrm{[P]} \\ A & \textrm{[N P]} \\ B & \textrm{[P M]} \\ \hline \end {array}\]
  • $x$ 与 $y$ 的点积 ($x \cdot y$) 需要 $P$ 次加法和 $P$ 次乘法，总共 $2P$ 次浮点运算 (FLOPs)。
  • 矩阵-向量乘积 $Ax$ 沿 $A$ 的每一行做 $N$ 次点积，总共 $2NP$ FLOPs。
  • 矩阵-矩阵乘积 $AB$ 对 $B$ 的 $M$ 列中的每一列做一个矩阵-向量乘积，总共 $2NPM$ FLOPs。
  • 一般来说，如果我们有两个高维数组 $C$ 和 $D$，其中一些维度是 收缩 (CONTRACTING) 的，一些是 批处理 (BATCHING) 的（例如 $C[\blue{GH}IJ\red{KL}], D[\blue{GH}MN\red{KL}]$），那么这种收缩的 FLOPs 成本是 $C$ 和 $D$ 的所有维度的乘积的两倍，其中批处理和收缩维度只计算一次（例如 $2\blue{GH}IJMN\red{KL}$）。注意，只有当维度同时出现在两个乘数中时，它才是批处理维度。（还要注意，如果没有收缩维度，这只是一个逐元素乘积，如果不适用因子 2）。
\[\begin{array}{ccc} \textrm{Operation} & \textrm{FLOPs} & \textrm{Data} \\ \hline x \cdot y & 2P & 2P \\ A x & 2NP & NP + P \\ AB & 2NPM & NP + PM \\ [c_0,...,c_N] \cdot [d_0,...,d_N] & 2 \prod c_i \times \prod_{\substack{d_j \notin \blue{BATCH} \\ d_j \notin \red{CONTRACT}}} d_j & \prod c_i + \prod d_j \\ \hline \end {array}\]

请注意，对于矩阵-矩阵乘法，计算按立方 $O(N^3)$ 缩放，而数据传输仅按平方 $O(N^2)$ 缩放——这意味着随着我们扩大 matmul 的规模，它变得 更容易 达到计算饱和极限。这是非常不寻常的，并在很大程度上解释了为什么我们使用由矩阵乘法主导的架构——它们易于扩展！

matmul-flops

前向和反向 FLOPs (Forward and reverse FLOPs)

在训练期间，我们要计算梯度。

如果我们想象 B 只是更大网络中的一个矩阵，而 A 是我们的输入激活，且 C = A B，则损失 L 对 B 的导数由链式法则给出：

\[\frac{\partial L}{\partial B} = \frac{\partial L}{\partial C}\frac{\partial C}{\partial B} = A^T \left(\frac{\partial L}{\partial C}\right)\]

这是一个外积，需要 $2NPM$ FLOPs 来计算（因为它收缩了 $N$ 维度）。同样，损失对 A 的导数是

\[\frac{\partial L}{\partial A} = \frac{\partial L}{\partial C}\frac{\partial C}{\partial A} = \left(\frac{\partial L}{\partial C}\right) B^T\]

也即又是 $2NPM$ FLOPs，因为 dL/dC 是一个大小为 $[N, M]$ 的（余）向量。

把这些加起来，我们看到 在训练期间，我们总共有 6NPM FLOPs，相比于推理期间的 2NPM：前向传递 2NPM，后向传递 4NPM。由于 PM 是矩阵中的参数数量，这是 Transformer 训练期间 FLOPs 的著名近似值 \(6 * \text{num parameters} * \text{num tokens}\) 的最简单形式：每个 token 需要 \(6 * \text{num parameters}\) FLOPs。我们将在下面展示更正确的推导。

Transformer 核算 (Transformer Accounting)

一个 Transformer 块通常包含：

  1. Self-attention (自注意力)
  2. MLP block (多层感知机块)

这是一个 Transformer 解码器架构的基本图表：

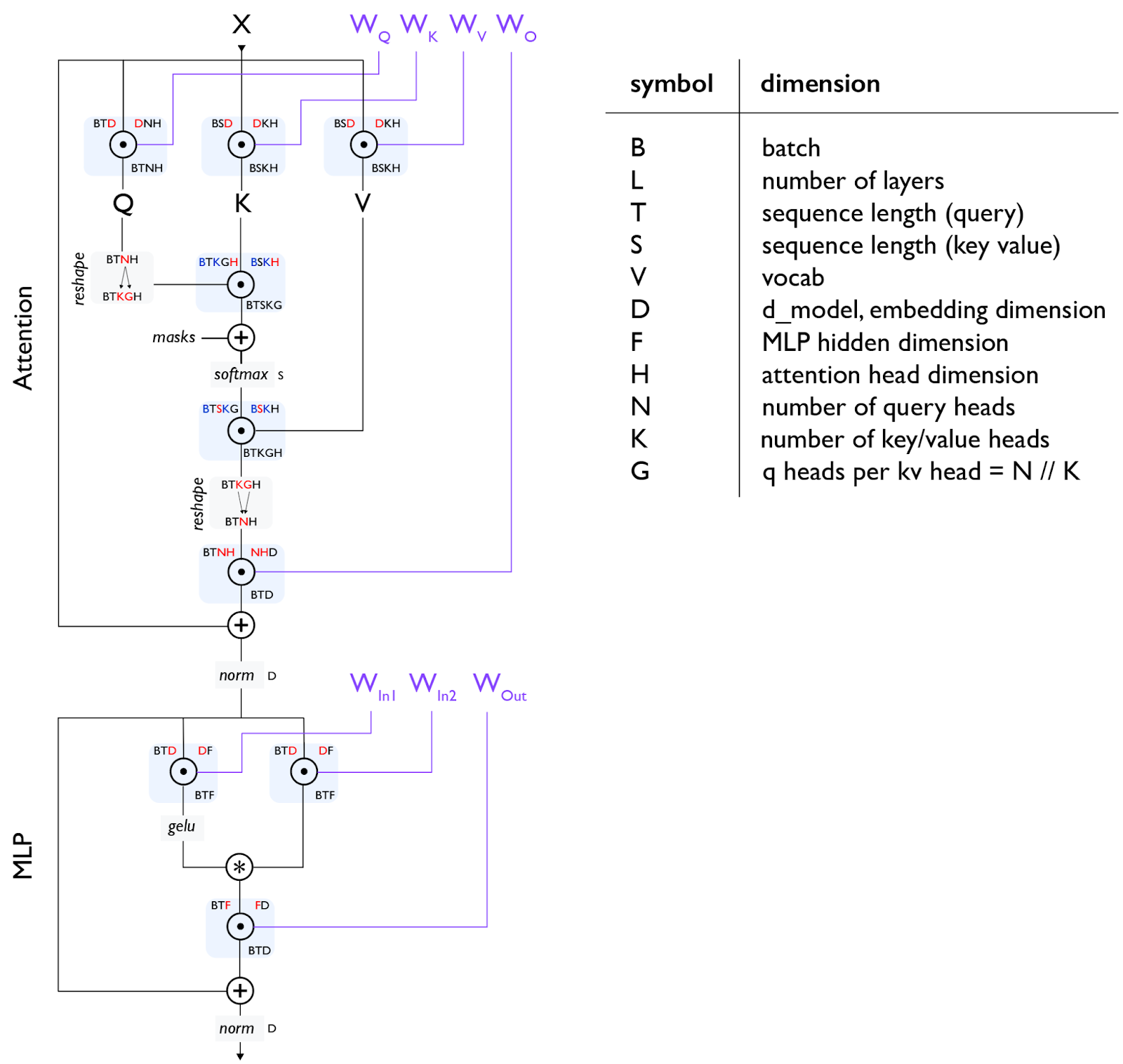transformer-diagram Figure: 此图显示了一个标准 Transformer 层，流程从上到下。我们使用单字母约定来描述 Transformer 中数组的形状和布局，再次以红色显示收缩维度，以蓝色显示批处理维度。在给定的操作中，输入形状位于左上角，参数形状位于右上角，结果形状位于下方，例如 BTD 是门控 einsum 的输入形状，DF 是权重形状。

注意 [gating einsum]: 上图使用“门控 einsums”1，其中我们将向上投影矩阵分成两个矩阵（上面的 $W_\text{In1}$ 和 $W_\text{In2}$），其输出被逐元素相乘作为一种“门控函数”。并非所有 LLM 都使用此功能，因此有时你会看到单个 $W_\text{In}$ 矩阵和总 MLP 参数计数为 2DF 而不是 3DF。

注意 2 [MHA attention]: 对于自注意力，T 和 S 是相同的，但对于交叉注意力，它们可能不同。对于普通的多头注意力 (MHA)，N 和 K 是相同的，而对于 Multi-Query Attention (MQA)2 K=1，对于 Grouped MQA (GMQA)3 K 仅需整除 N。

全局 FLOPs 和参数计算 (Global FLOPs and Params Calculation)

由于下面的计算，我们将计算每层 FLOPs，以避免到处放置 L 因子。

MLPs

Transformer 的 MLP 通常由 2 个输入 matmuls 组成，它们被逐元素组合，以及一个输出 matmul：

\[\begin{array}{ccc} \textrm{operation} & \textrm{train FLOPs} & \textrm{params} \\ \hline \\ A[B,T,\red{D}] \cdot W_{in1}[\red{D}, F] & 6BTDF & DF \\[10pt] A[B,T,\red{D}] \cdot W_{in2}[\red{D}, F] & 6BTDF & DF \\[10pt] \sigma\left(A_{in1}\right)[B,T, F] * A_{in2}[B,T, F] & \gray{O(BTF)} \\[10pt] A[B,T,\red{F}] \cdot W_{out}[\red{F}, D] & 6BTDF & DF \\[10pt] \hline \\ & \approx 18BTDF & 3DF \end{array}\]

Attention

对于具有不同 Q 和 KV 头数的通用分组查询注意力情况，让我们假设 Q,K,V 投影具有相等的头维度 H，并估计 QKVO matmuls 的成本：

\[\begin{array}{ccc} \textrm{operation} & \textrm{train FLOPs} & \textrm{params} \\ \hline \\ A[B,T,\red{D}] \cdot W_{Q}[\red{D}, N, H] & 6BTDNH & DNH \\[10pt] A[B,T,\red{D}] \cdot W_{K}[\red{D}, K, H] & 6BTDKH & DKH \\[10pt] A[B,T,\red{D}] \cdot W_{V}[\red{D}, K, H] & 6BTDKH & DKH \\[10pt] A[B,T,\red{N}, \red{H}] \cdot W_{O}[\red{N}, \red{H}, D] & 6BTDNH & DNH \\[10pt] \hline \\ & 12BTD(N+K)H & 2D(N+K)H \end{array}\]

点积注意力操作更微妙，实际上也是 \(TH \cdot HS\) matmul 在 \(B\), \(K\) 维度上批处理，一个 softmax，以及一个 \(TS \cdot SH\) matmul 再次在 \(B\), \(K\) 维度上批处理。我们以蓝色突出显示批处理维度：

\[\begin{array}{cc} \textrm{operation} & \textrm{train FLOPs} \\ \hline \\[3pt] Q[\blue{B}, T, \blue{K}, G, \red{H}] \cdot K[\blue{B}, S, \blue{K}, \red{H}] & 6BTSKGH = 6BTSNH \\[3pt] \textrm{softmax}_S \;\; L[B, T, S, K, G] & \gray{O(BTSKG) = O(BTSN)} \\[3pt] S[\blue{B}, T, \red{S}, \blue{K}, G] \cdot V[\blue{B}, \red{S}, \blue{K}, H] & 6BTSKGH = 6BTSNH \\[3pt] \hline \\ & \approx 12BTSNH = 12BT^2NH \\ \end{array}\]

注意 [因果掩码]: 最近的大多数 Transformer 使用因果掩码而不是全双向注意力。在这种情况下，点积运算的有效 FLOPs 减少了 1/2。为了在实践中实现这种减少，我们需要利用注意力内核，而不是简单的 einsum。

其他操作 (Other Operations)

Transformer 中还会发生其他几个操作。Layernorms 相对便宜，对于一阶成本估计可以忽略不计。还有最终巨大的（虽然不是每层都有）unembedding 矩阵乘法。

\[\begin{array}{ccc} \textsf{operation} & \textsf{train FLOPs} & \textsf{params} \\ \hline \\ \textrm{layernorm}_D \;\; A[B,T,\red{D}] & \gray{O\left(BTD\right)} & \gray{D} \\[10pt] A[B,T,\red{D}] \cdot W_{unembed}[\red{D}, V] & 6BTDV & DV \\ \end{array}\]

Transformer FLOPs 的一般经验法则 (General rule of thumb for Transformer FLOPs)

如果我们忽略较短上下文训练的点积注意力成本，那么所有层的总 FLOPs 为

\[\begin{align*} (18BTDF + 12BTD(N+K)H)L = 6 *BT * (3DF + 2D(N+K)H)L \\ = 6 * \textrm{num tokens} * \textrm{parameter count} \end{align*}\]

导致了用于估计密集 Transformer FLOP 计数的著名经验法则，忽略了注意力 FLOPs。（Unembedding 是另一个简单的 matmul，具有 $6BSDV$ FLOPs 和 $DV$ 参数，遵循相同的经验法则。）

随上下文长度变化的注意力分数成本 (Fractional cost of attention with context length)

如果我们确实考虑上面的点积注意力，并假设 \(F=4D\), \(D=NH\)（如同典型情况）和 \(N=K\)：

\[\small{\frac{\textrm{attention FLOPs}}{\textrm{matmul FLOPs}} = \frac{12BT^2NH}{18BTDF + 24BTDNH} = \frac{12BT^2D}{4*18 BTD^2 + 24 BTD^2} = \frac{12BT^2D}{96 BTD^2} = \frac{T}{8D}}\]

所以结论是 点积注意力 FLOPs 仅在 T>8D 时才在训练期间占主导地位。对于 D ~ 8k，这将是 ~64K tokens。这在某种程度上有道理，因为这意味着随着 MLP 大小的增加，注意力 FLOPs 变得不那么关键。Flash Attention 也有助于缓解长上下文的成本，我们在 附录 A 中简要讨论。

杂项数学 (Miscellaneous Math)

稀疏性和混合专家 (Mixture-of-Experts)

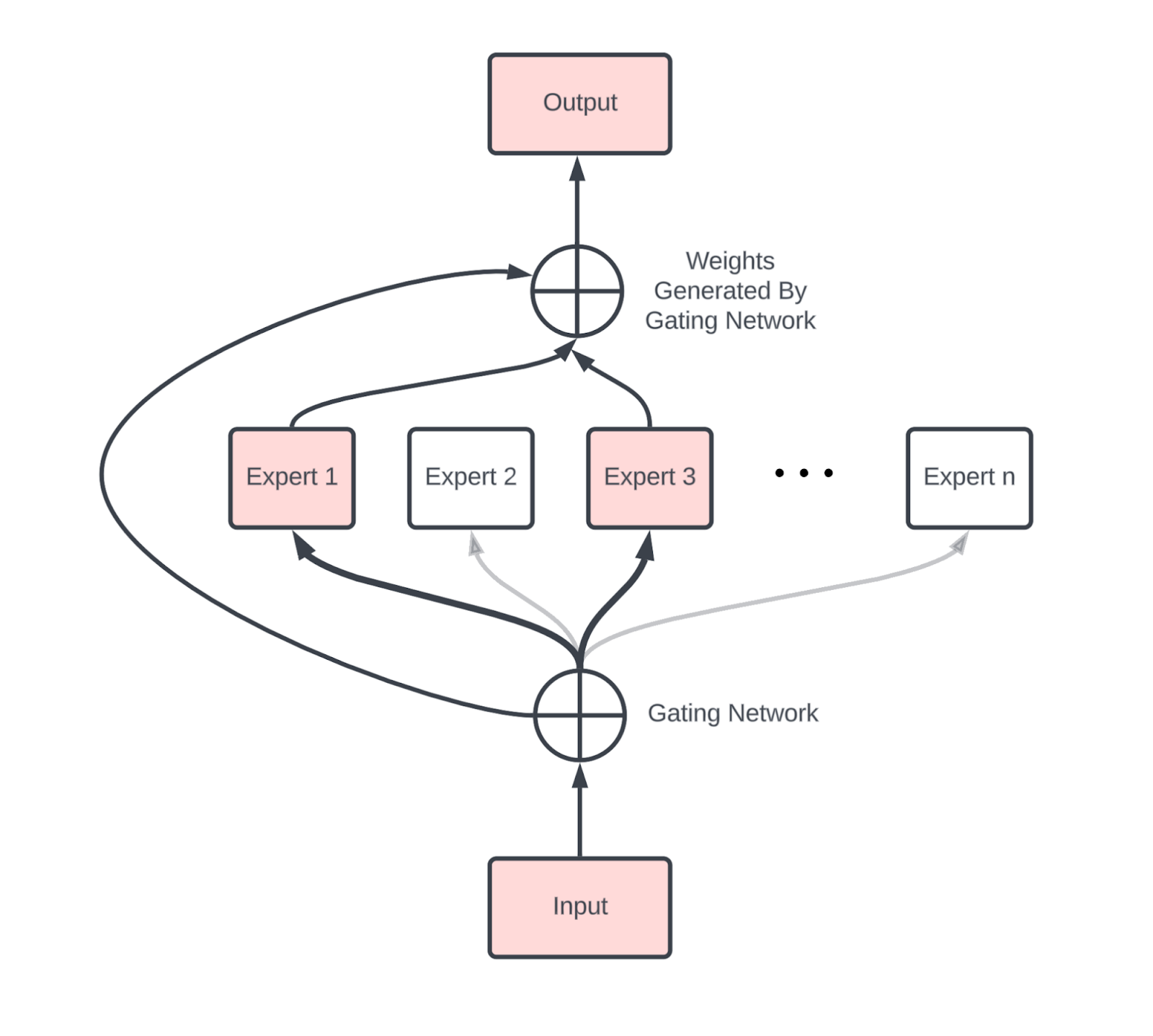
忽略混合专家 (MoE) 模型4将是失职的，该模型将标准 Transformer 中的单个密集 MLP 块替换为一组可以在其间动态路由的独立 MLP。作为一阶近似，MoE 只是每层有 E 个 MLP 块的普通密集模型，而不是仅仅一个。每个 token 激活 $k$ 个专家，通常 $k=2$。这增加了 $O(E)$ 的参数计数，同时相比密集版本将每个 token 激活的总参数数量乘以 $k$。

moe

梯度检查点 (Gradient checkpointing)

反向传播作为一种算法用内存换取计算。反向传播不需要 \(O(n_\text{layers}^2)\) FLOPs，它需要 \(O(n_\text{layers})\) 内存，保存前向传递期间生成的所有中间激活。虽然这通过计算优于二次方，但在内存方面极其昂贵：如果一个模型 \(B * T=4M\)（每批次 4M 总 token），L=64，D=8192，避免所有不必要的反向传递计算，必须保存大约 \(2 * 20 * B * T * D * L = 84TB\) 的 bfloat16 激活。

为了避免保存这么多内存，我们可以选择仅保存一部分中间激活。这里有一些我们使用的策略。

  • Block remat: 确切地保存每层的输入。这是我们使用的最激进的方法，每层只保存 1 个检查点，对于上面的例子意味着我们只保存 4.2TB。这迫使我们在反向传递中重复基本上所有的前向传递 FLOPs，这意味着我们将 FLOPs 从 \(6ND\) 增加到大约 \(8ND\)。
  • Big matmuls only: 另一个简单的策略是只保存大 matmuls 的输出。这让我们避免在反向传递期间重新计算任何大 matmuls，但仍然让我们重新计算其他激活函数和部分注意力。这将每层 20 减少到接近每层 7。

这绝不是全面的。使用 JAX 时，这些通常由 jax.remat/jax.checkpoint 控制（你可以 在此 阅读更多信息）。

键值 (KV) 缓存 (Key-Value caching)

正如我们在 第 7 节 中看到的，LLM 推理有两个关键部分，预填充 (prefill) 和生成 (generation)。

  • Prefill 处理长提示并将其注意力激活保存在键值缓存 (KV Cache) 中以用于生成，特别是注意力块中的键值投影。
  • Generation 将几个这些 KV 缓存批处理在一起，并从每个缓存中采样 token。

每个 KV 缓存实际上是一个大小为 $[2, S, L, K, H]$ 的数组，其中 2 考虑了键和值。这相当大！int8 中的 Key-Value 缓存的总大小为 $2SLKH$。对于具有 8k 上下文长度、64 层和 $KH = NH = D = 8192$ 的中等大小模型，这就是 $2 \cdot 8192 \cdot 64 \cdot 8192 = 8\text{GiB}$。你可以看到为什么我们会想要使用 $K \ll N$ 的 GMQA。

你应该从本节学到什么？ (What Should You Take Away from this Section?)

  • Transformer 的总体参数和 FLOPs 相当容易计算，并在下面总结（假设 MHA，批量大小 B，词汇表大小 V，长度 T 的序列，D=dmodel，F=dff）：
Component Params per layer Training FLOPs per layer
MLP 3DF 18BTDF
Attention 4DNH 24BTDNH + 12BT2NH
Other D BTD
Vocab DV (total, not per-layer) 12BTDV
  • MLP 块的参数计数主导总参数计数，并且只要序列长度 $T < 8D$，MLP 块也主导 FLOPs 预算。
  • 对于合理的上下文长度，训练期间的总 FLOPs 预算可以很好地近似为 \(6 \cdot \text{num_params} \cdot \text{num_tokens}\)。
  • 在推理期间，我们的 KV 缓存每个缓存大约 \(2 \cdot S \cdot L \cdot N \cdot H\)，尽管架构修改通常可以减少这一点。

一些练习题 (A Few Problems to Work)

Question 1: 一个 $D=4096$, $F=4 \cdot D$, $V=32,000$, 和 $L=64$ 的模型有多少参数？其中有多少比例是注意力参数？每个 token 的 KV 缓存有多大？你可以假设 $N\cdot H=D$ 和 int8 KVs 的多头注意力。

点击这里查看答案。
  1. 总参数大致为 \(L \cdot (3DF + 4DNH + D) + 2DV\)。对于给定的数字，这是 \(64 \cdot (3 \cdot 4e3 \cdot 16e3 + 4 \cdot 4e3 \cdot 4e3 + 4e3) + 2 \cdot 4e3 \cdot 32e3 = 16e9\)，或 16B 参数。
  2. 一般而言，注意力参数与总参数的比率为 \(4DNH / (4DNH + 3DF) = 4D^2 / (4D^2 + 12D^2) = 1/4\)。这意味着大约 1/4 的参数用于注意力。
  3. 每个 token，我们的 KV 缓存是 \(2 \cdot L \cdot N \cdot H = 2 \cdot 64 \cdot 4096\) (int8)，即 512kB / token。

Question 2: 在 {‘X': 4, ‘Y': 8, ‘Z': 4} 上执行 A[BX, DY] *D W[DY, F] 需要多少总 FLOPs？每个 TPU 执行多少 FLOPs？

点击这里查看答案。

操作的总“理论” FLOPs 是 \(2 \cdot B \cdot D \cdot F\)。然而，因为计算没有跨 Z 维度分片，我们实际上做了 Z 倍的额外 FLOPs，意味着总共 \(2 \cdot B \cdot D \cdot F \cdot Z\) FLOPs。由于计算跨其他维度分片，每设备总数大致为 \(2 \cdot B \cdot D \cdot F / (X \cdot Y)\)。

Question 3: 执行 $A[I,J,K,L] * B[I,J,M,N,O] \rightarrow C[K,L,M,N,O]$ 涉及多少 FLOPs？

点击这里查看答案。

遵循上面的规则，我们有 I 和 J 作为收缩维度，K, L, M, N, 和 O 作为非收缩维度。我们没有“批处理维度”，所以这只是 \(2 \cdot I \cdot J \cdot K \cdot L \cdot M \cdot N \cdot O\)，所有轴的乘积。如果我们有一个共享轴，它只会被计算一次。

Question 4: 自注意力的算术强度是多少（忽略 Q/K/V/O 投影）？给出作为 Q 和 KV 长度 T 和 S 的函数的答案。 在什么上下文长度下注意力是 FLOPs 受限的？

点击这里查看答案。

我们的总字节数是 \(2 * \text{sizeof}(Q) + 2 * \text{sizeof(K or V)} = 4BTNH + 4BSKH = 4BHK * (TG + S)\)，总 FLOPs 是 \(4BTSNH + O(BTSN)\)，算术强度是 \(4BTSKGH / (4BHK * (TG + S))\)。 本质上，随着 S 非常大，这趋向于 G。

Question 5: 在什么序列长度下，自注意力 FLOPs 等于 QKVO 投影 FLOPs？

点击这里查看答案。

纯粹是 \(24BTDNH == 12BT^2NH\) 何时成立的问题。简化得到 \(2D = T\)，例如对于 \(D=4096\)，这是 \(8192\)。这告诉我们对于大多数合理的上下文长度，matmul FLOPs 更大。

Question 6: 假设我们在前向传递期间每层只保存 7 个主要 matmuls (Q, K, V, O + 三个 FFW 矩阵) 的输出。我们在反向传递期间需要“重物化 (rematerialize)”多少额外 FLOPs？

点击这里查看答案。

保存这七个 matmul 输出意味着反向传递必须重新计算两个注意力 matmuls：\(QK^{\top}\) 和 \(\operatorname{softmax}(QK^{\top})V\)。每个都是 $T \times T$ matmul，在 $B$ 序列和 $N$ 头上批处理，所以额外的 FLOPs 是 \(4 \; B \, T^{2} \, N \, H\)。

Question 7: DeepSeek v3 称它在 14.8T tokens 上训练了 2.79M H800 hours。鉴于它有 37B 激活参数，他们大致达到了什么硬件利用率？提示：注意他们使用了 FP8 FLOPs 且没有结构化稀疏性。

点击这里查看答案。

从 H800 规格表中，我们发现了 3,026 TFLOPs/s 的 FP8 性能（带稀疏性），或者不带稀疏性通常是一半（1.513e15 FLOPs/s）。2.79M H800 hours 意味着 2.79e6 * 1.513e15 * 60 * 60 = 1.52e25 总 FLOPs。鉴于 37B 的激活参数计数，这次训练运行应该使用了大约 6 * 37e9 * 14.8e12 = 3.3e24 FLOPs。这意味着 FLOPs 利用率约为 3.3e24 / 1.52e25 = 21.7%。

Appendix A: Flash Attention 是如何工作的？

传统的反对将 Transformer 扩展到非常长上下文的观点是，注意力 FLOPs 和内存使用量随上下文长度呈二次方增长。Flash Attention 的基本思想是以 K/V 块计算注意力，我们计算局部 softmax 和一些辅助统计数据，然后将它们传递给下一个块，下一个块将它们与其局部块结合起来。

flash-algo

从硬件角度来看，这让我们将 Q 的块放入 VMEM（上面的算法称为片上 SRAM），这样我们只需在每次迭代时加载 KV 块，从而降低算术强度。

脚注

来源

Transformer Math - Part 4

  1. GLU variants improve transformer quality. ↩︎

  2. Fast transformer decoding: One write-head is all you need. ↩︎

  3. GQA: Training generalized multi-query transformer models from multi-head checkpoints. ↩︎

  4. Outrageously large neural networks: The sparsely-gated mixture-of-experts layer. ↩︎