这是 DeepMind Scaling Book 系列的第 5 部分。

如何并行化训练 Transformer (How to Parallelize a Transformer for Training)

How To Scale Your Model Part 5 (Part 4: Transformer Math | Part 6: Training LLaMA)

在这里，我们讨论 LLM 训练中使用的四种主要并行方案：数据并行 (data parallelism)、完全分片数据并行 (fully-sharded data parallelism, FSDP)、张量并行 (tensor parallelism) 和流水线并行 (pipeline parallelism)。对于每一种，我们计算在什么点上我们会受到通信瓶颈的限制。

我们所说的 Scaling 是指什么？ (What Do We Mean By Scaling?)

“模型扩展 (model scaling)”的目标是能够增加用于训练或推理的芯片数量，同时实现吞吐量的成比例、线性增加（我们称之为 强扩展 (strong scaling)）。虽然单个芯片上的性能取决于内存带宽和 FLOPs 之间的权衡，但集群层面的性能取决于通过与有用的 FLOPS 重叠来隐藏芯片间通信。这并非易事，因为增加芯片数量会增加通信负载，同时减少我们可以用来隐藏通信的每设备计算量。正如我们在 第 3 节 中看到的，分片矩阵乘法通常需要昂贵的 AllGathers 或 ReduceScatters，这可能会阻止 TPU 做有用的工作。本节的目标是找出这些操作何时变得 太昂贵。

在本节中，我们将讨论四种常见的并行方案：(纯) 数据并行 (data parallelism)、完全分片数据并行 (fully-sharded data parallelism) (FSDP / ZeRO 分片)、张量并行 (tensor parallelism) (也称为模型并行) 和 (简要) 流水线并行 (pipeline parallelism)。对于每一种，我们将展示我们产生什么通信成本，以及该成本在什么点上开始成为我们计算成本的瓶颈 1。

对于本节，你可以只关注芯片间通信成本，因为只要我们有足够大的单芯片批量大小，从 HBM 到 MXU 的数据传输就已经与计算重叠了。我们将使用以下符号来简化本节的计算：

Notation Meaning (model parameters)
D dmodel (隐藏层维度/残差流维度)
F dff (前馈层维度)
B 批处理维度 (批次中的 token 总数，不是每设备的)
T 序列长度
L 模型层数
Notation Meaning (hardware characteristic)
C 每芯片 FLOPS/s
W 网络带宽 (双向，通常带下标，例如 $W_{\text{ici}}$ 或 $W_{\text{dcn}}$
X 沿网格轴 X 的芯片数
Y 沿另一个网格轴 Y 的芯片数
Z 沿第三个网格轴 Z 的芯片数

为了简单起见，我们将 Transformer 近似为一堆 MLP 块——正如我们在 第 4 节 中看到的，对于较大的模型，注意力是 FLOPs 相对较小的一部分。如果不进行并行化，我们的简单 Transformer 层的算法如下：

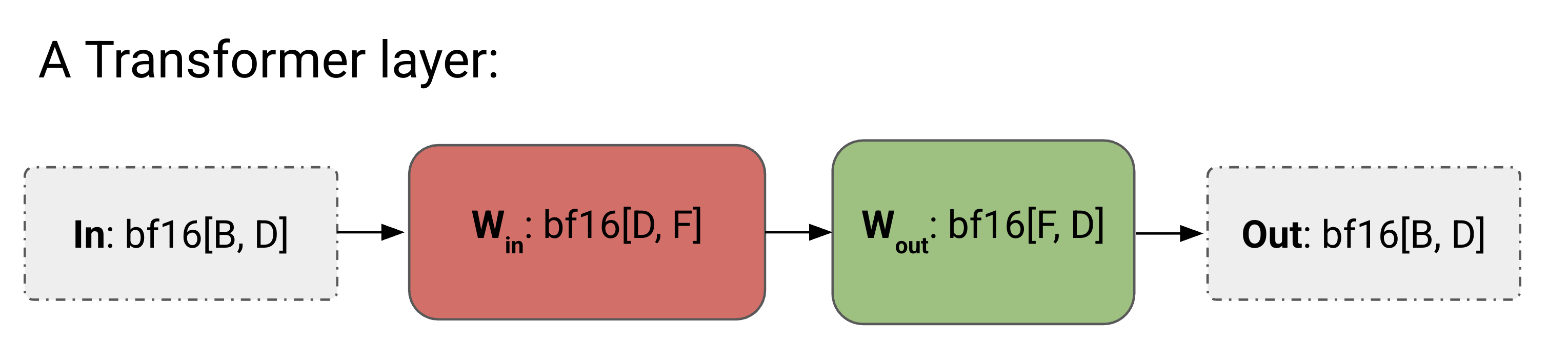
transformer-layer

点击这里查看我们没有并行化的小 Transformer 的完整算法。

前向传播: 需要计算 Loss[B]

  1. Tmp[B, F] = In[B, D] *D Win[D, F]
  2. Out[B, D] = Tmp[B, F] *F Wout[F, D]
  3. Loss[B] = …

反向传播: 需要计算 dWout[F, D], dWin[D, F]

  1. dOut[B, D] = …
  2. dWout[F, D] = Tmp[B, F] *B dOut[B, D]
  3. dTmp[B, F] = dOut[B, D] *D Wout[F, D]
  4. dWin[D, F] = In[B, D] *B dTmp[B, F]
  5. dIn[B, D] = dTmp[B, F] *F Win[D, F] (前一层需要)

我们提供这个是为了与添加通信的算法进行比较。

以下我们将讨论 4 种并行方案。每个方案都可以看作是上图中 In, Win, Wout, 和 Out 的分片的唯一定义。

1. Data parallelism: 激活沿 batch 分片，参数和优化器状态在每个设备上复制。通信仅在反向传递期间发生。

\[\text{In}[B_X, D] \cdot_D W_\text{in}[D, F] \cdot_F W_\text{out}[F, D] \rightarrow \text{Out}[B_X, D]\]

2. Fully-sharded data parallelism (FSDP or ZeRO-3): 激活沿 batch 分片（像纯数据并行一样），参数沿相同网格轴分片，并在前向传递中使用前及时 AllGather。优化器状态也沿 batch 分片。减少重复内存。

\[\text{In}[B_X, D] \cdot_D W_\text{in}[D_X, F] \cdot_F W_\text{out}[F, D_X] \rightarrow \text{Out}[B_X, D]\]

3. Tensor parallelism (also called Megatron sharding or model parallelism): 激活沿 D ($d_\text{model}$) 分片，参数沿 F ($d_{ff}$) 分片。在每块前后 AllGather 和 ReduceScatter 激活。与 FSDP 兼容。

\[\text{In}[B, D_Y] \cdot_D W_\text{in}[D, F_Y] \cdot_F W_\text{out}[F_Y, D] \rightarrow \text{Out}[B, D_Y]\]

4. Pipeline parallelism: 权重沿层维度分片，激活微批处理并沿层维度滚动。流水线阶段之间的通信极小（只是在单跳上传输激活）。滥用符号：

\[\text{In}[L_Z, B, D][i] \cdot_D W_\text{in}[L_Z, D, F][i] \cdot_F W_\text{out}[L_Z, F, D][i] \rightarrow \text{Out}[L_Z, B, D][i]\]

数据并行 (Data Parallelism)

Syntax: \(\text{In}[B_X, D] \cdot_D W_\text{in}[D, F] \cdot_F W_\text{out}[F, D] \rightarrow \text{Out}[B_X, D]\)

当你的模型可以在单个芯片上容纳即使是很小的 batch size（>240 tokens，以便计算受限）时，你应该始终使用简单的数据并行。 纯数据并行将我们的激活拆分到任意数量的 TPU 上，只要 TPU 的数量小于我们的 batch size。前向传递不涉及通信，但在每一步结束时，每个 TPU 对其本地梯度执行 AllReduce 以在更新参数之前同步它们。

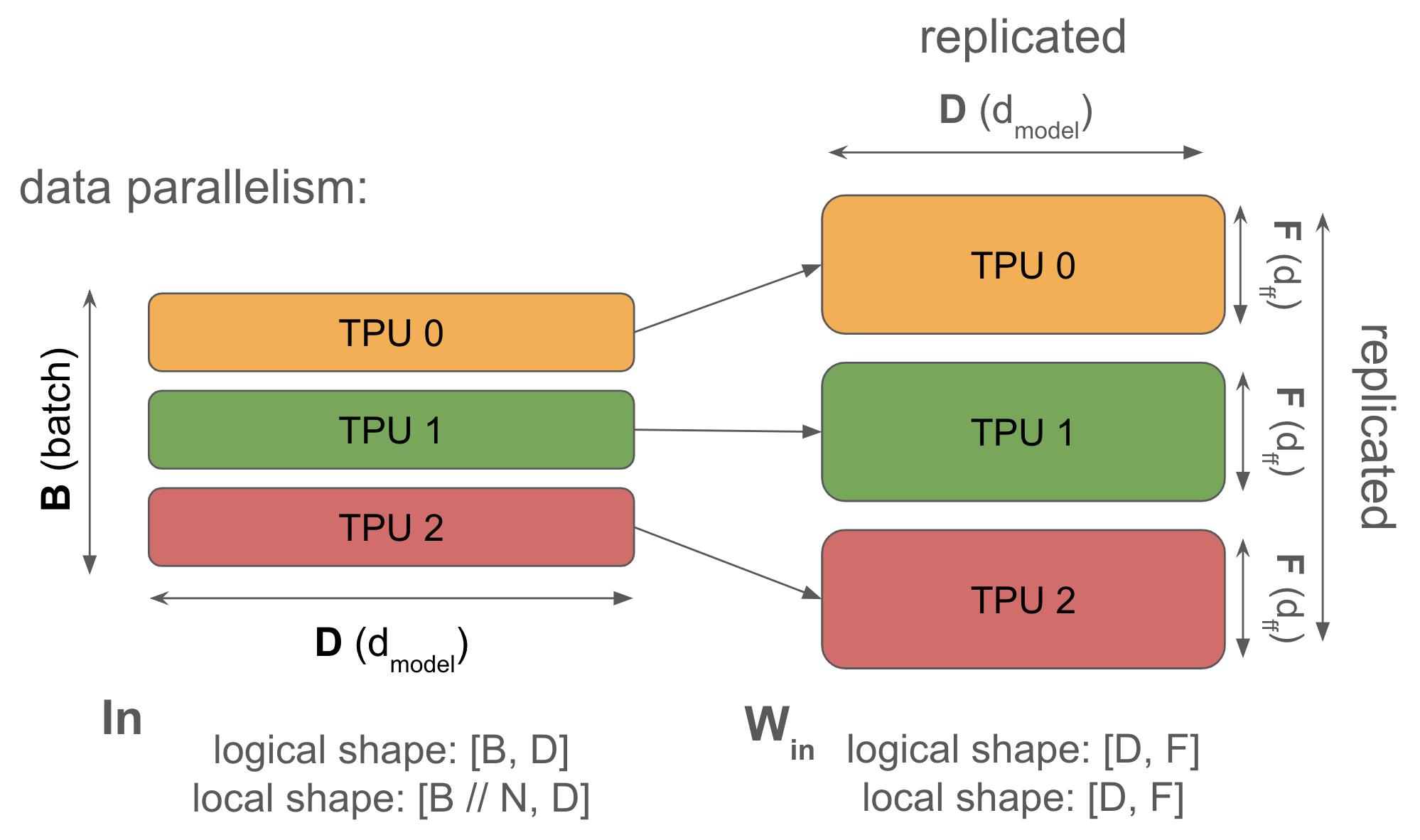
data-parallelism

点击这里查看前向和反向传递的完整算法。

纯数据并行算法:

前向传播: 需要计算 Loss[BX]

  1. Tmp[BX, F] = In[BX, D] *D Win[D, F]
  2. Out[BX, D] = Tmp[BX, F] *F Wout[F, D]
  3. Loss[BX] = …

反向传播: 需要计算 dWout[F, D], dWin[D, F]

  1. dOut[BX, D] = …
  2. dWout[F, D] {UX} = Tmp[BX, F] *B dOut[BX, D]
  3. dWout[F, D] = AllReduce(dWout[F, D] {UX}) (不在关键路径上，可以异步完成)
  4. dTmp[BX, F] = dOut[BX, D] *D Wout[F, D]
  5. dWin[D, F] {UX} = In[BX, D] *B dTmp[BX, F]
  6. dWin[D, F] = AllReduce(dWin[D, F] {UX}) (不在关键路径上，可以异步完成)
  7. dIn[BX, D] = dTmp[BX, F] *F Win[D, F] (前一层需要)

注意前向传递没有通信——全部在反向传递中！反向传递还有一个很好的属性，即 AllReduces 不在“关键路径”中，这意味着每个 AllReduce 可以在方便的时候执行，并且不会阻止你执行后续操作。如果总通信成本超过我们的总计算成本，它 仍然会成为瓶颈，但从实现的角度来看，它更加宽容。我们将看到模型/张量并行不具备此属性。

为什么要这样做？ 纯数据并行通过在 batch 维度上拆分我们的激活来减少激活内存压力，允许我们只要有更多芯片来拆分 batch 维度就可以几乎任意增加 batch size。特别是在训练期间，当我们的激活通常主导我们的内存使用时，这非常有帮助。

为什么不这样做？ 纯数据并行对于减少模型参数或优化器状态的内存压力毫无作用，这意味着纯数据并行对于参数 + 优化器状态无法放入单个 TPU 的大规模有趣模型很少有用。

我们何时受到通信瓶颈的限制？

我们成为计算受限的条件是 \(T_\text{math}/T_\text{comms} > 1\)，或者当

\[\begin{align} \frac{B}{X} > \frac{C}{W_\text{ici}}. \end{align}\]

结论是，为了在数据并行中保持计算受限，我们需要每设备 batch size \(B / X\) 超过 ICI 运算强度，$C / W_\text{ici}$。

完全分片数据并行 (Fully-Sharded Data Parallelism, FSDP)

Syntax: \(\text{In}[B_X, D] \cdot_D W_\text{in}[D_X, F] \cdot_F W_\text{out}[F, D_X] \rightarrow \text{Out}[B_X, D]\)

完全分片数据并行（通常称为 FSDP 或 ZeRO 分片）将模型优化器状态和权重拆分到数据并行分片上，并在需要时有效地 gather 和 scatter 它们。与纯数据并行相比，FSDP 极大地减少了每设备内存使用量，并节省了反向传递 FLOPs，开销极小。

fsdp

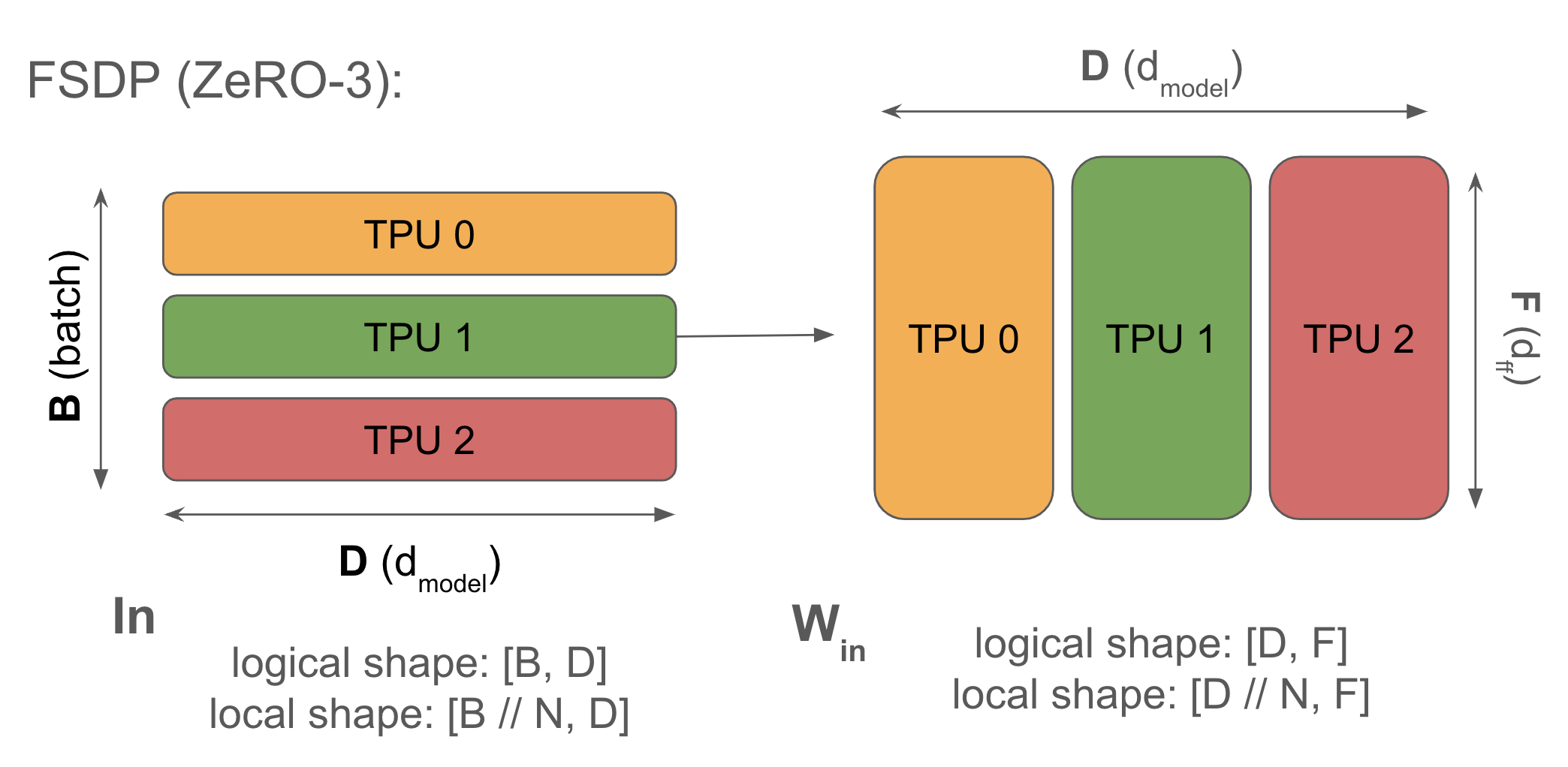
点击这里查看 FSDP 的完整算法。

Fully-Sharded Data Parallelism (FSDP):

前向传播: 需要计算 Loss[BX]

  1. Win[D, F] = AllGather(Win[DX, F]) (不在关键路径上，可以在上一层期间做)
  2. Tmp[BX, F] = In[BX, D] *D Win[D, F] (现在可以丢弃 Win[D, F])
  3. Wout[F, D] = AllGather(Wout[F, DX]) (不在关键路径上，可以在上一层期间做)
  4. Out[BX, D] = Tmp[BX, F] *F Wout[F, D]
  5. Loss[BX] = …

反向传播: 需要计算 dWout[F, DX], dWin[DX, F]

  1. dOut[BX, D] = …
  2. dWout[F, D] {UX} = Tmp[BX, F] *B dOut[BX, D]
  3. dWout[F, DX] = ReduceScatter(dWout[F, D] {UX}) (不在关键路径上，可以异步完成)
  4. Wout[F, D] = AllGather(Wout[F, DX]) (可以提前完成)
  5. dTmp[BX, F] = dOut[BX, D] *D Wout[F, D] (在此处可以丢弃 Wout[F, D])
  6. dWin[D,F] {UX} = dTmp[BX, F] *B In[BX, D]
  7. dWin[DX, F] = ReduceScatter(dWin[D, F] {UX}) (不在关键路径上，可以异步完成)
  8. Win[D, F] = AllGather(Win[DX, F]) (可以提前完成)
  9. dIn[BX, D] = dTmp[BX, F] *F Win[D, F] (前一层需要) (在此处可以丢弃 Win[D, F])

我们何时受到通信瓶颈的限制？

\[T \approx 4 \cdot D \cdot F \cdot \max\left(\frac{B}{X \cdot C}, \frac{1}{W_\text{ici}}\right)\]

因此，与纯数据并行一样，当 \(B / X > C / W_\text{ici}\) 时，我们是计算受限的。

Takeaway: 当每设备 batch size 小于 $2550 / M_X$ 时，FSDP 和纯数据并行都会受到带宽限制，其中 $M_X$ 是网格轴的数量。

张量并行 (Tensor Parallelism)

Syntax: \(\text{In}[B, D_Y] \cdot_D W_\text{in}[D, F_Y] \cdot_F W_\text{out}[F_Y, D] \rightarrow \text{Out}[B, D_Y]\) (we use \(Y\) to eventually combine with FSDP)

在完全分片数据并行 AllReduce 中，我们在芯片间移动权重。我们也可以分片模型的前馈维度并在层期间移动激活——这被称为“1D 模型并行”或 Megatron 分片。这可以解锁每 pod 更小的有效 batch size。

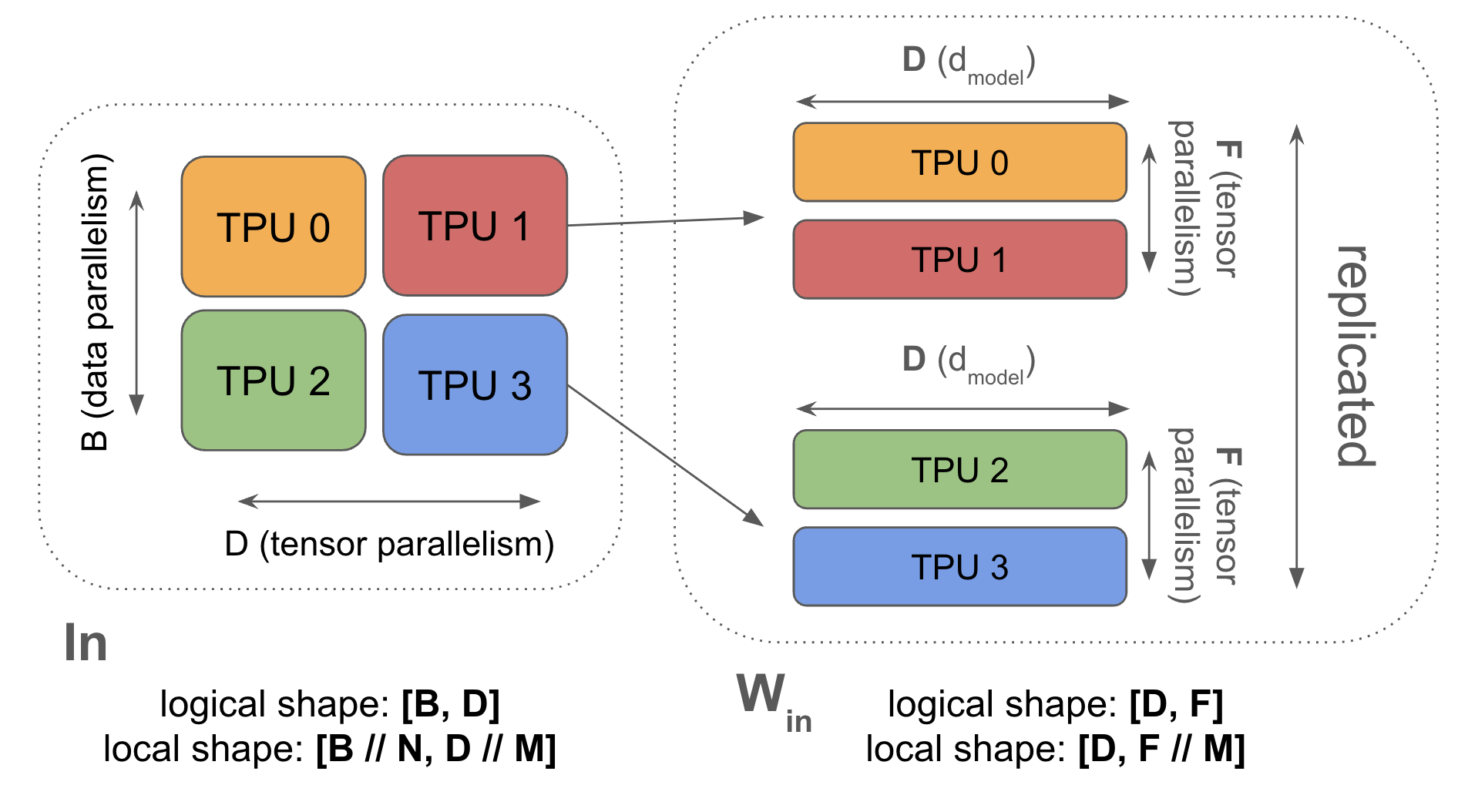
model-parallelism

点击这里查看张量并行的算法！

Tensor Parallelism:

前向传播: 需要计算 Loss[B]

  1. In[B, D] = AllGather(In[B, DY]) (在关键路径上)
  2. Tmp[B, FY] = In[B, D] *D Win[D, FY] (沿收缩未分片，所以无通信)
  3. Out[B, D] {UY} = Tmp[B, FY] *F Wout[FY, D]
  4. Out[B, DY] = ReduceScatter(Out[B, D] {UY}) (在关键路径上)
  5. Loss[B] = …

反向传播: 需要计算 dWout[FY, D], dWin[D, FY]

  1. dOut[B, DY] = …
  2. dOut[B, D] = AllGather(dOut[B, DY]) (在关键路径上)
  3. dWout[FY, D] = Tmp[B, FY] *B dOut[B, D]
  4. dTmp[B, FY] = dOut[B, D] *D Wout[FY, D] (在此处可以丢弃 dOut[B, D])
  5. In[B, D] = AllGather(In[B, DY]) (这可以通过与前向传递中的 (1) 共享来跳过)
  6. dWin[D, FY] = dTmp[B, FY] *B In[B, D]
  7. dIn[B, D] {U.Y} = dTmp[B, FY] *F Win[D, FY] (前一层需要)
  8. dIn[B, DY] = ReduceScatter(dIn[B, D] {U.Y}) (在关键路径上)

这有多昂贵？

\[\frac{F}{Y \cdot C} > \frac{1}{W_\text{ici}}\]

因此，例如，对于 TPUv5p，$C / W_{ici} = 2550$ (bf16)，所以我们只能做张量并行直到 $Y < F / 2550$。当我们有多个 ICI 轴时，我们的 $T_\text{comms}$ 减少了 $M_Y$ 倍，所以我们得到 $Y < M_Y \cdot F / 2550$。

Takeaway: 当 $Y > M_Y \cdot F / 2550$ 时，张量并行变得受通信限制。对于大多数模型，这是 8 到 16 路张量并行。

结合 FSDP 和张量并行 (Combining FSDP and Tensor Parallelism)

Syntax: \(\text{In}[B_X, D_Y] \cdot_D W_\text{in}[D_X, F_Y] \cdot_F W_\text{out}[F_Y, D_X] \rightarrow \text{Out}[B_X, D_Y]\)

FSDP 和张量并行很好的一点是它们可以结合使用。通过沿两个轴分片 Win 和 Wout，我们既节省了内存又节省了计算。

mixed-fsdp-model-parallelism

点击这里查看混合 FSDP + 张量并行的完整算法。

前向传播: 需要计算 Loss[B]

  1. In[BX, D] = AllGatherY(In[BX, DY]) (在关键路径上)
  2. Win[D, FY] = AllGatherX(Win[DX, FY]) (可以提前完成)
  3. Tmp[BX, FY] = In[BX, D] *D Win[D, FY]
  4. Wout[FY, D] = AllGatherX(Wout[FY, DX]) (可以提前完成)
  5. Out[BX, D] {U.Y} = Tmp[BX, FY] *F Wout[FY, D]
  6. Out[BX, DY] = ReduceScatterY(Out[BX, D] {U.Y}) (在关键路径上)
  7. Loss[BX] = …

（反向传播类似，为了简洁省略）

什么是 FSDP 和 TP 的正确组合？ 简单的准则是 FSDP 移动权重，张量并行移动激活。这意味着随着我们的 batch size 缩小（尤其是当我们做更多数据并行时），张量并行变得更便宜，因为我们的每分片激活更小。

Takeaway: 一般来说，在训练期间，FSDP 的最佳数量是 \(X_{opt} = \sqrt{\frac{B}{F} \frac{M_X}{M_Y} N}\)。

Takeaway: 结合张量并行和 FSDP 允许我们将 $B/N$ 降低到 \(2550^2 / 2F\)。这让我们处理每芯片低至 100 的 batch，这大约比仅仅使用 FSDP 可以实现的要小八倍。

下面是一个交互式动画，展示了不同 batch size 下的总计算时间和通信时间：

注意：这里嵌入了原书的 plot，本地可能无法直接交互，由于跨域限制。

流水线 (Pipelining)

你可能已经注意到我们在前面的章节中完全避免谈论流水线。流水线是 GPU 并行的主导策略，但在 TPU 上稍微不那么重要。简而言之，流水线训练包括将模型的层拆分到多个设备上，并在前向和反向传递期间在流水线阶段之间传递激活。

为什么这是个好主意？ 流水线之所以好是因为流水线阶段之间的通信成本低，这意味着即使使用低带宽互连也可以训练非常大的模型。这在 GPU 上通常非常有用。

为什么这很难/烦人？ TPU 0 几乎总是空闲的！这被称为流水线气泡。通常我们通过微批处理来缓解这个问题。

跨 Pod 扩展 (Scaling Across Pods)

最大的 TPU 切片是 TPU v5p SuperPod，有 8960 个芯片。当我们想要扩展超过这个大小时，我们需要跨越数据中心网络 (DCN) 边界。

Takeaway: 只要我们的每 pod batch size 至少为 71k tokens，使用纯数据并行跨多个 TPU pod 扩展就相当简单。

TPU 上 LLM 训练的要点 (Takeaways from LLM Training on TPUs)

  • 增加并行度或减小 batch size 都倾向于使我们更加受通信限制，因为它们减少了每芯片执行的计算量。
  • 在训练期间，我们要考虑 4 种主要的并行方案（数据并行、FSDP、张量并行）。
Strategy Description
Data Parallelism 激活是 batch 分片的，其他所有都是完全复制的，我们在反向传递期间 all-reduce 梯度。
FSDP 激活、权重和优化器是 batch 分片的，权重在使用前被 gathered，梯度被 reduce-scattered。
Tensor Parallelism (aka Megatron, Model) 激活沿 \(d_\text{model}\) 分片，权重沿 \(d_{ff}\) 分片，激活在 Win 之前 gathered，结果在 Wout 之后 reduce-scattered。
Mixed FSDP + Tensor Parallelism 上述两者的结合，其中 FSDP gather 模型分片权重。
  • 纯数据并行很少有用，因为模型及其优化器状态使用字节 = 10x 参数计数。
  • 数据并行和 FSDP 在 \(\text{batch size per shard} < C / W\) 时变得受通信限制。
  • 张量并行在 \(\lvert Y\rvert > F / 2550\) 时变得受通信限制。对于大多数模型，这是大约 8-16 路。
  • 混合 FSDP + 张量并行允许我们将 batch size 降低到 \(2550^2 / 2F \approx 100\)。

一些练习题 (Some Problems to Work)

让我们使用 LLaMA-2 13B 作为本节的基础模型。

Question 1: LLaMA-2 13B 有多少参数？

点击这里查看答案。
  • FFW 参数: \(3LDF\) = 8.5e9
  • Attention 参数: \(4DNHL\) = 4.2e9
  • Vocabulary 参数: \(2VD\) = 0.3e9
  • Total: 8.5e9 + 4.2e9 + 0.39e9 = 13.1e9，不出所料！

Question 2: 假设我们使用 BS=16M tokens 和 Adam 进行训练。忽略并行性，模型的参数、优化器状态和激活总共使用多少内存？

点击这里查看答案。

参数 (bf16) 和两个优化器状态 (fp32) 的总内存为 (2 + 4 + 4) * 13e9 ~ 130GB。前两个 matmuls 后的激活形状为 $BF$，最后一个为 $BD$，所以 bf16 的总内存为 2 * 40 * 16e6 * 5,120 * (1 + 2 * 2.7) ~ 4.2e13 = 42TB。

Question 3: 假设我们想在 TPUv5p 16x16x16 切片上以 32k 序列长度和 3M tokens 的总 batch size 进行训练。假设如上所述使用 bfloat16 权重和 float32 优化器。

  1. 我们可以使用纯数据并行吗？
  2. 我们可以使用纯 FSDP 吗？
  3. 我们可以使用混合 FSDP + 张量并行吗？如果可以，$X$ 和 $Y$ 应该是什么？
点击这里查看答案。

  1. 我们不能使用纯数据并行，因为它在每个芯片上复制参数和优化器状态，这已经大约 130GB，超过了我们每芯片的 HBM (96GB)。

  2. 让我们从内存方面看。使用 3M 而不是 16M，我们得到 ~7.86e12 总检查点激活，加上 1.3e11 优化器状态，这使我们几乎正好达到 8TB。TPUv5p 切片总共有 393TB HBM，所以我们在 HBM 限制内。接下来看我们是否受通信限制。使用 4096 个芯片和 3 个并行轴，我们可以做的最小 batch size 是 850 * 4096 = 3.48M tokens。这略高于我们的 3M batch size。所以我们实际上是受通信限制的。所以一般答案是 不，我们不能单独做 FSDP。

  3. 现在我们知道主要问题是受通信限制，所以让我们代入一些数字。首先，我们知道混合 FSDP + 张量并行的每芯片 batch size 需要高于 $2550^2 / 2F = 235$。这意味着我们理论上可以做到！ 我们有规则 $X_{opt} = \sqrt((F / B) * (M_X / M_Y) * N)$，所以这里即使是 sqrt(3e6 * 2 * 4096 / 13824) = 1333，意味着我们将做大约 1024 路 DP 和 4 路 TP。

Appendix A: Deriving the backward pass comms

上面，我们将 Transformer 层前向传递简化为 Out[B, D] = In[B, D] *D Win[D, F] *F Wout[F, D]。我们如何推导反向传递所需的通信？

点击这里查看推导。
  1. dWout[F, D] = Tmp[B, F] *B dOut[B, D]
  2. dTmp[B, F] = dOut[B, D] *D Wout[F, D]
  3. dWin = dTmp[B, F] *B Tmp[B, F]
  4. dIn[B, D] = dTmp[B, F] *F Win[D, F]

注意这些公式是数学陈述，没有提到分片。反向传递的工作是计算这四个量。所以要弄清楚所需的通信，我们只需采用上述四个方程中要进行 matmul 的所有量（Tmp, dOut, Wout, Win）的分片，这些分片由我们的并行化方案指定，并使用分片 matmuls 的规则来弄清楚我们需要做什么通信。

脚注

来源

Training at Scale - Part 5

  1. 我们将专注于通信边界。 ↩︎